I was intrigued by the title of a post at The American Thinker blog by Jason Kissner, titled: “Bayes’ Theorem and Mr. Obama’s Literary Agency.” Dr. Kissner is reported to hold a Ph. D. in criminology. Bayes’ Theorem is a result from probability theory. The Wikipedia article gives one interpretation1 of it: “it expresses how a subjective degree of belief should rationally change to account for evidence.” “Obama’s Literary Agent” refers to a 1991 publicist’s author portfolio brochure that says Barack Obama was born in Kenya.
I’m a mathematician by training and in graduate school I taught math and graded papers. I thought I’d see if there were something I could grade in this paper at The American Thinker. In order to grade a paper, one must first get inside what the writer is saying and understand the argument. I’ll save everyone a lot of time and say that Dr. Kissner concludes that the answer to how likely it is Obama was born in Kenya is about 50%, which is remarkable, to say the least.
I’ll try to guide you through that process and I guess I need to explain a little about conditional probability first.
Statisticians like to represent outcomes or events by capitol letters taken from the first part of the alphabet and they use the letter “P” to mean “probability of.” When we talk about probability, the old standby is the idealized coin toss. So if the outcome is “the coin comes up heads” is labeled “A,” then the probability of that outcome is written “P(A)”. Probabilities are expressed by a number between 0 (can’t happen) and 1 (must happen). For our coin toss, the probability is 0.5, and we would write P(A) = 0.5.
“Conditional probability” is the probability of an event considering or conditioned on other information. We write “P (A|B)” and read “probability of A given B.” An event not happening is denoted with a “not” symbol as in “¬A.” So let’s say that event A is that a voter votes for Obama and that event B is that a voter is Republican. The P(A) might be around 0.5, but P(A|B) is much smaller, and Bayes’ Theorem gives a way to calculate it. Below is the “extended” version of Bayes’ Theorem that is used by Dr. Kissner:
One can estimate the probabilities in the preceding example by sampling (polling) and arrive at a reasonable answer. The voodoo comes in when dealing with questions where we don’t have hard estimates, where things are subjective. In these cases, there is room for monkey business, hence the quotation popularized by Mark Train: “There are three kinds of lies: lies, damned lies, and statistics.”
The American Thinker article asks: what is the probability of Barack Obama being born in Kenya, given that his 1991 publisher wrote in a brochure that he was? Or as they put it, how much does the “new evidence” of the publishers brochure change a former estimate of the probability.
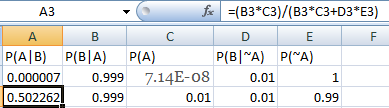
Kissner’s reader is asked to quantify their current opinion of the probability that Obama was born in Kenya. To arrive at my estimate, I will use just two pieces of evidence: 1) The Hawaii Department of Health says he was born in Hawaii and 2) the Immigration and Naturalization Service reports that no US citizen (e.g. Obama’s mother) traveled from Kenya to the United States by air in the entire year around Obama’s birth. Given that there is only one known published instance of vital records fraud in Hawaii, I am going to be generous and say that there was another one in 1961, so the possibility of Obama having a fraudulent birth registration is about 1 in 14,000 births. The INS report is completely independent of Hawaiian birth records, and I would estimate the probability that the report is wrong about the number of air travelers from Kenya at 1 in 1,000. Because the events are independent, the individual probabilities may be multiplied and the resulting probability that Obama was born in Kenya based on those two pieces of evidence alone is 0.00000007.
I’m going to finish my own calculation at this point. We need P(B|A), the probability that the literary agent wrote Obama was born in Kenya given that he was. 0.999 is a reasonable number: If Obama were born in Kenya, then you would expect the agent to get it right. Next we need P(B|¬A), the probability that the literary agent wrote that Obama was born in Kenya given that he wasn’t. Considering that Barack Obama Sr. was born in Kenya, I would put the probability of a mistake by the agent saying that Barack Obama Jr. was born there at maybe 1 in 100, or .01. So with that we can do the calculation. The answer is that the probability that President Obama was born in Kenya is 0.000007, which is a far cry from 0.5. Why the difference?
The American Thinker article points the way by saying,
The … the calculation can certainly be framed in different ways which are open to debate
My estimate of the starting probability that Obama was born in Kenya is much lower than Kissner’s. He says 0.01, but while my estimate is reasoned, his is based on, believe it or not, the probability that the Colts will win Super Bowl XLVII.
If readers think, on the basis of evidence other than the Breitbart disclosure, that Obama is far less likely to have been born in Kenya than the Colts are to win Super Bowl XLVII, they can revise their prior downward accordingly.
Pulling a number out of the air like that is not going to make me disposed towards awarding partial credit.
Kissner assigns P(B|A) a value of 0.9999. That’s not unreasonable, nor that far from my own estimate. He assigns P(B|¬A) a value of 0.01, which I can hardly argue with since it’s my number too. And from those he correctly comes up with about 0.5; even replacing .9999 with my value of .999, the answer still rounds to 0.5.
 The evidence of the publicist brochure makes it more likely that Obama was born in Kenya (50 – 100 times more likely using Kissner’s and my figures respectively), but the overwhelming difference in results is based on the estimate of how likely that Obama was born in Kenya before we ever heard of the promotional brochure. In the end, the application of Bayes’ Theorem does little to illuminate the question, and in fact obscures bias in initial assumptions in a avalanche of words and calculations and the fact that the most important number in the calculation, the initial probability, was pulled out of thin air.
The evidence of the publicist brochure makes it more likely that Obama was born in Kenya (50 – 100 times more likely using Kissner’s and my figures respectively), but the overwhelming difference in results is based on the estimate of how likely that Obama was born in Kenya before we ever heard of the promotional brochure. In the end, the application of Bayes’ Theorem does little to illuminate the question, and in fact obscures bias in initial assumptions in a avalanche of words and calculations and the fact that the most important number in the calculation, the initial probability, was pulled out of thin air.
1Bayes’ Theorem is a theoretical mathematical result. There are differing interpretations as to what it might mean in the real world. One faction are the Bayesians, and the statement I quoted is of their view.
I used this spreadsheet for the calculations:

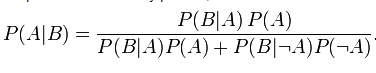



I’d like to see if his Kenyan birth probability changes knowing the New York Times said Obama was born in Hawaii… before the publishers brochure came out.
Did you factor in the probability given that the copy writer has admitted the reference in question was probably a mistake as it was not based on information gathered from a reliable source?
Will this be on the test?
Someone on HuffPo criticized me recently for unconditionally accepting the “0 US citizens traveling from Kenya” number as gospel. His belief is that
1) “zero” is an impossibly low number — no US citizens traveled to or from Kenya at all in 12 months? — and
2) the US was not tracking foreign travel in 1961 the way they do in our post-9/11 era, citing his ability to freely drive between the US and Canada without even showing ID pre-9/11 (I suspect this would really be “first WTC bombing,” when things really started tightening up).
The improbability of the number being zero, point 1, supposedly is a strong indicator that point 2 must be true.
My own belief is that point 2 is probably wrong: that there’s a big difference between flying to a non-North American country and driving across the Canadian border, and that the US was probably very diligent about tracking the former, even that long ago. But I don’t know, so is the probability that the number of US citizens traveling to Kenya was truly 0 as high as .999?
(I will note that chart itself explicitly says, “Exclusive of Canadian travel over land borders,” so clearly that was considered to be the exceptional case.)
Even if this number were not as high as .999, I would still want to plug in other numbers capturing the number of times Barack Obama himself has ever been on record as saying he was born in Kenya (zero), vs. the number of times he’s said he was born in Hawaii (lots, including at least four interviews when he became HLR president, and of course his autobiography).
These latter points speak directly to Breitbart’s contention that this was an intentional statement perpetrated by Obama. Since every other place where Obama himself has said where he was born, he has said “Hawaii.” I would place a very low value on Obama having told his literary agent, “go ahead, say ‘Kenya'”, and an even lower value on the error being intentionally continued on the web site for a dozen years after his Hawaii-sayin’ autobiography was published.
Written customs declarations for arriving international air and sea passengers date back many decades. Trans-Atlanttic passengers iin the Titanic era filled them in. The little cards were turned in on arrival and were archived.
The question is: might someone who travelled from Kenya to London and stopped over there before boarding a plane to the US just say they had been in Europe? I suppose it’s possible. .
But travelling with a infant is a different matter. Someone arriving in the US with an infant needs to show eiither that the infant is a US citizen or, if the child is a foreign citizen, that they have the appropriate visa for the infant to live here. That’s true whether it is your natural child or an adoptee.
More precisely there were zero by air. There was a non-zero number by boat, but I have excluded that possibility because of the time required. The fact that there were persons counted by sea indicates that they were counting, and I would think the comprehensiveness of air travel counts would be at least as good as counts of sea arrivals. Even if we put the estimate of INS error at 1 in 10 instead of 1 in 1000, I can just add a contemporary notation in the Obama immigration file to boost it back to the same starting number.
No, I didn’t factor that in, although one could certainly do that. If I spent the time, I could probably reduce the probability of a Kenyan birth by several orders of magnitude. But hey, what’s the difference between “wildly improbable” and “virtually impossible”?
An arriving international passenger has to show a passport, and that would have an Kenyan exit stamp.
There’s a reason why we call it “The American Stinker”
According to the birthers I know:
“Wildly improbable” means even a five year old knows it happened, and you’re a fool if you think otherwise.
“Virtually impossible” means it happened but was covered up.
Somehow the realism level of this modeling reminded me of this:
http://xkcd.com/704/
Five letters.
“I was told there wouldn’t be any math”
Chevy Chase, channelling President Ford.*
I muddled through statistics and probability as best I could, which is to say, just barely.
Please forgive me if this is a silly question, but: Isn’t the probability that President Obama was born in Kenya, or anywhere other than Hawaii actually 0, since the event has already happened?
I never understood how probability could be applied to something which already happened.
*The same President Ford who was adopted. His original name was Leslie King. His biological father beat his mother, and a few days after the future president was born, threatened to kill the baby, his wife, and the nursemaid with a knife. She left and divorced him, eventually remarrying Mr. Ford. Mr. King never supported his son – his own father paid Ford’s mother child support on his behalf.
Birthers, who seem to love to play amateur psychiatrist, always point to Obama’s upbringing as if it was unique or strange. Even among the tiny set of people who have been president of the United States, Obama isn’t unique in this regard.
“what is the probability of Barack Obama being born in Kenya, given that his 1991 publisher wrote in a brochure that said he was?”
That’s the probability they want to study? What the heck did they supposedly quantify! I can’t stop laughing …… LOL!
It’s a great article, Doc, will finish up when I recover!!!
Canada and the US had a specific “cross-border” agreement that allowed free land travel for each others citizens.
That sort of agreement is explicit. Normal immigration processes apply to any country of origin for which there is no specific agreement. Kenya had no such agreement with the US.
The reference you quoted in that chart alludes to the agreement with Canada that existed at that time
Interesting and informative — thanks!
It’s later, I’m tired, less likely to crack up. Made it through, though barely held on over the bit about the Super Bowl. Vegas run on such chuckleheads.
Even a modest grasp of probability (among many other things!) would innoculate one against birtherism.
The 50% probability claim reminds me of the fuzzy pseudo-science offered by Creation Design proponents. “The eyeball is too complex to have been developed without a higher power designing it” is in a structural sense somewhat like saying the Kenyan birth is proven by an isolated document. Both assertions let you skirt responsibility for doing an empirical analysis. I know it’s not germane to the current discussion, but I’m interested in how much if any crossover there is between Birthers, Truthers, Young Earth Creationists, ObamaCare Death Panelists,Survivalists, Gunowners Believing Obama Would Take their Guns Away, and all the other stimulating people.
You can easily remove the “if any”! The set of people buying into all of it must be small (in %age of population terms), but I doubt there are any progressive, leftist, intellectual birthers. There are far-left Truthers … an example of how the political spectrum is anything but 1-dimensional. If you go extreme enough, you bunmp into all the other extremists!
Anyway, yes, there are many intersections in the hyperdimensional Venn diagram of conservative / libertarian delusions! Spend some time talking to birthers, other subjects will come up. When it comes to people, nuts are always mixed (in my experience).